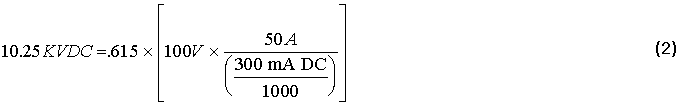Technology Transfer Network
Emission Measurement Center Spectral Database
Fuel Oil Fired Electricity Utility Boiler Emission Test
|
LONG ISLAND LIGHTING CORPORATION NORTHPORT, NEW YORK EPA Contract No. 68D20163 Work Assignment No. I-34 Prepared by: Research Division Entropy, Inc. Post Office Box 12291 Research Triangle Park, North Carolina 27709 Prepared for: Lori Lay U. S. Environmental Protection Agency Emissions Measurement Branch Research Triangle Park, North Carolina 27711 April 29, 1994 DISCLAIMER This document was prepared by Entropy, Inc. under EPA Contract No. 68D20163, Work Assignment No. I-34. This document has been reviewed by the U.S. Environmental Protection Agency (EPA). The opinions, conclusions, and recommendations expressed herein are those of the authors, and do not necessarily represent those of EPA. Mention of specific trade names or products within this report does not constitute endorsement by EPA or Entropy, Inc. TABLE OF CONTENTS 1.0 INTRODUCTION 1.1 BACKGROUND 1.2 DESCRIPTION OF THE PROJECT 1.3 PROJECT ORGANIZATION 2.0 PROCESS DESCRIPTION AND SAMPLE POINT LOCATIONS 2.1 FACILITY DESCRIPTION 2.3 SAMPLE POINT LOCATIONS 3.0 RESULTS 3.1 OBJECTIVES AND TEST MATRIX 3.2 FIELD TEST CHANGES AND PROBLEMS 3.3 SUMMARY OF RESULTS 4.0 SAMPLING AND ANALYTICAL PROCEDURES 4.1 EXTRACTIVE SYSTEM FOR DIRECT GAS PHASE ANALYSIS 4.2 SAMPLE CONCENTRATION 4.3 CONTINUOUS EMISSION MONITORING 4.4 FLOW DETERMINATIONS 4.5 PROCESS DATA 4.6 ANALYTICAL PROCEDURES 5.0 INTERNAL QUALITY ASSURANCE/QUALITY CONTROL ACTIVITIES 5.1 QC PROCEDURES FOR MANUAL FLUE GAS TEST METHODS 5.2 QC PROCEDURES FOR INSTRUMENTAL METHODS 5.3 QA/QC CHECKS FOR DATA REDUCTION, VALIDATION, AND REPORTING 5.4 CORRECTIVE ACTIONS 6.0 CONCLUSIONS 7.0 REFERENCES APPENDICES NOTE: Appendices A-D are not available 1.0 INTRODUCTIONThe U. S. Environmental Protection Agency (EPA) Office of Air Quality Planning and Standards (OAQPS), Industrial Studies Branch (ISB), and Emission Measurement Branch (EMB) directed Entropy, Inc. to conduct an emission test at the Unit 1 oil-fired boiler at Long Island Lighting Company's (LILCO) electric generating station in Northport, New York. The test was conducted on July 19 to July 21, 1993. The purpose of this test was to identify which hazardous air pollutants (HAPs) listed in the Clean Air Act Amendments of 1990 are emitted from this source. The measurement method used Fourier transform infrared (FTIR) spectrometry, which had been developed for detecting and quantifying many organic HAPs in a flue gas stream. Besides developing emission factors (for this source category), the data will be included in an EPA report to Congress. Before this test program, Entropy conducted screening tests using the FTIR method at facilities representing several source categories, including a coal-fired boiler. These screening tests were part of the FTIR Method Development project sponsored by EPA to evaluate the performance and suitability of FTIR spectrometry for HAP emission measurements. These tests helped determine sampling and analytical limitations, provided qualitative information on emission stream composition, and allowed estimation of the mass emission rates for a number of HAPs detected at many process locations. The evaluation demonstrated that gas phase analysis using FTIR can detect and quantify many HAPs at concentrations in the low part per million (ppm) range and higher, and a sample concentration technique was able to detect HAPs at sub-ppm levels. Following the screening tests, Entropy conducted a field validation study at a coal-fired steam generation facility to assess the effectiveness of the FTIR method for measuring HAPs, on a compound by compound basis. The flue gas stream was spiked with HAPs at known concentrations so that calculated concentrations, provided by the FTIR analysis, could be compared with actual concentrations in the spiked gas stream. The analyte spiking procedures of EPA Method 301 were adapted for experiments with 47 HAPs. The analytical procedures of Method 301 were used to evaluate the accuracy and precision of the results. Separate procedures were performed to validate a gas phase analysis technique and a sample concentration technique of the FTIR method. A complete report, describing the results of the field validation test, has been submitted to EPA[1]. This report was prepared by Entropy, Inc. under EPA Contract No. 68D20163, Work Assignment No. I-34. Research Triangle Institute (RTI) provided the process information given in Sections 2.1 and 3.3.3. 1.2 DESCRIPTION OF THE PROJECT The FTIR-based method uses two different sampling techniques: (1) direct analysis of the extracted gas stream (hereafter referred to as the gas phase technique or gas phase analysis) and (2) sample concentration followed by thermal desorption. Gas phase analysis involves extracting gas from the sample point location and transporting the gas through sample lines to a mobile laboratory where sample conditioning and FTIR analysis are performed. The sample concentration system employs 10 g of Tenax® sorbent, which can remove organic compounds from a flue gas stream. Organic compounds adsorbed by Tenax® are then thermally desorbed into the smaller volume of the FTIR absorption cell; this technique allows detection of some compounds down to the ppb level in the original sample. For this test, approximately 850 dry liters of flue gas were sampled during each run using the sample concentration system. Section 4.0 describes the sampling systems. Entropy operated a mobile laboratory (FTIR truck) containing the instrumentation and sampling equipment. The truck was driven to the site at Northport, and parked within reach of both locations. Three test runs were performed over a two-day period. Entropy tested the flue gas from the inlet and the outlet of one of the electrostatic precipitators (ESP). The furnace burned fuel oil No. 6. Section 2.0 contains descriptions of the process and the sampling point locations. FTIR gas phase analysis was used to measure carbon monoxide (CO), carbon dioxide (CO2), sulfur dioxide (SO2), nitrogen oxides (NOx), and ppm levels of other species. EPA instrumental test methods were used to provide concentrations of CO, CO2, O2, and hydrocarbons (HC). The sample concentration technique was used to measure HAPs at ppb levels. Entropy conducted three 4-hour sample concentration runs. During each run samples were collected simultaneously at the inlet and outlet of the control device. Gas phase analysis was used to test both locations sequentially concurrent with each sample concentration run. Combustion gas volumetric flows were determined by performing velocity traverses during each run. Section 3.1 gives the test schedule. The test program was funded and administered by the Industrial Studies Branch (ISB) and the Emissions Measurement Branch (EMB) of the U.S. EPA. A representative from RTI collected process data. The following list presents the organizations and personnel involved in coordinating and performing this project.
LILCO Corporate Ms. Linda Bergeron (516) 391-6136
Contacts: Mr. Paul Lynch (516) 391-6135
Northport Facility Mr. James Brennan (516) 262-2200
Coordinators: Mr. Jack Tiernan (516)
EMB Work Assignment Ms. Lori Lay (919) 541-4825
Managers: Mr. Dennis Holzschuh (919) 541-5239
ISB Contacts: Mr. Kenneth Durkee (919) 541-5425
Mr. William Maxwell (919) 541-5430
Entropy Project Manager: Dr. Thomas Geyer (919) 781-3551
Entropy Test Personnel: Mr. Scott Shanklin
Dr. Laura Kinner
Ms. Lisa Grosshandler
Mr. Mike Worthy
Dr. Ed Potts
Dr. Grant Plummer
Mr. Rick Straughsbaugh
RTI Representative: Mr. Jeffrey Cole (919) 990-8606
2.0 PROCESS DESCRIPTION AND SAMPLE POINT LOCATIONSLong Island Lighting Company's (LILCO) Northport One powerplant in Northport, New York is located in Suffolk County about 30 miles from New York City. Unit One is an oil-fired (residual, No. 6) base-loaded unit that normally operates 24 hours a day, 7 days a week, except for a 2- to 3-week planned outage for maintenance every 18 months. Although Unit One is technically a base-loaded unit, a better characterization would be a load- following unit. The unit operates from approximately 25 to 100 percent capacity (100 to 385 MWe) depending on the need for power. Fuel is supplied to the plant through an offshore platform where oil tankers can dock and transfer their oil. The source of oil varies but the oil is sampled and analyzed prior to acceptance for delivery, upon delivery, and once a week in as-burned grab samples. Table 2-1 shows the oil analysis results for both days the plant was tested. During this test, Unit One oil consumption averaged 389.2 gal/min. During startup, Unit One is fired by distillate (No. 2) oil until the operating temperature is achieved. At this time, residual oil is gradually substituted until only residual oil is burned. Northport One uses a tangentially-fired, dry bottom furnace to produce 2,550,000 lb/hr of steam for a General Electric steam turbine generator rated at 385 MWe. A tangentially-fired furnace uses windboxes at the four corners of the furnace to introduce fuel and air into the combustion zone (see Figure 2-1). Combustion air is supplied by a forced draft fan and ducted through the air preheater where the temperature of the air is increased. Both fuel and preheated combustion air are projected from the corners of the furnace along a line tangential to a small circle moving in a horizontal plane at the center of the furnace. The fuel and combustion air are ignited by an electric spark from gas igniters in the windboxes. The flame zone extends from the corners of the furnace to the center where the fireball swirls. The fuel nozzles can be tilted upward or downward as a means of temperature control. Steam temperature is also controlled by gas recirculation, which involves diverting a portion of the exhaust gases after the economizer and reintroducing them at the bottom of the furnace. Normal operating temperature in the furnace is approximately 1700-1800 degF. Flue gas from the combustion process passes through the superheater, primary and secondary gas reheaters, and the economizer. From the economizer, the majority of flue gas (a portion being ducted through the gas recirculation system) is ducted through the air preheater and to the electrostatic precipitator (ESP). The flow is divided before passing through the two ESP sections. At the ESP outlet, the separated flows are channeled through two identical induced draft (ID) fans rated at 1,020,000 acfm (at 285 degF). The two streams join at the base of the 600-ft stack and the flue gas is exhausted to the atmosphere through the 16.75-ft stack exit diameter. 2.2 AIR POLLUTION CONTROL DEVICES 2.2.1 Nitrogen Oxides (NOx) Control The tangentially-fired unit is by design a low NOx unit. This NOx reduction is accomplished thorough mixing of air and fuel in the combustion chamber. The unit also uses close couple overfire air (CCOFA) for NOx control. Using CCOFA involves redistributing the combustion air introduced into the furnace to reduce combustion temperatures. 2.2.2 Sulfur Dioxide (SO2) Control To control SO2 emissions LILCO uses No. 6 fuel oil with a maximum of one percent sulfur, by weight. 2.2.3 Particulate Control A cold-side ESP is used to collect the flyash exiting the air preheaters. The total collection area and the specific collection area (SCA) of the ESP are 206,640 ft2 and 189 ft2/1000 acfm, respectively. The ESP has 4 fields in 4 parallel chambers resulting in 16 cells. The flue gas is divided into two streams before entering the separate A and B sections of the ESP. These sections consist of 4 fields in 2 parallel chambers resulting in 8 cells (Figure 2-2). During the test only the inlet and outlet of the B section (South) were monitored. A rapping system is used to dislodge dust from the ESP plates and into dust hoppers. The plates are rapped at different times in a sequence designed to minimize the amount of particulate re-entering the gas stream. The FTIR truck was parked at a position along the process within 150 ft of the ESP inlet and outlet sample point locations. This enabled Entropy to perform gas phase sampling sequentially between the two locations. Figure 2-3 is an overall schematic showing both test locations. 2.2.1 ESP Inlet Sampling was performed at the inlet to the South-side ESP (Figure 2-4). Six 4-inch diameter sample ports were available at a location downstream of the air preheater and upstream of the South-side ESP inlet. The ports were equally spaced along the top of a horizontal section of the duct 30 feet above ground level. Access was provided by stairs, ladder, and a catwalk. The probes sampled flue gas from the middle two ports at a depth near the center of the duct. One hundred fifty feet of heated sample line were used to connect the gas phase probe to the sample pump in the FTIR truck. 2.2.2 ESP Outlet Four 4-inch diameter sample ports were available at a location downstream of the South-side ESP and induced draft (ID) fan (Figure 2-5). The ports were equally spaced along a section of the duct that was angled at about 45 deg from vertical. This location was about 30 feet above ground level. Access was provided by stairs, and a catwalk. Scaffolding was erected on the catwalk to provide access to the ports. Flue gas was extracted from the middle two ports at a depth near the center of the duct. One hundred feet of heated sample line were used to connect the gas phase sample probe to the sample pump in the FTIR truck. 3.0 RESULTS3.1 OBJECTIVES AND TEST MATRIX The purpose of the test program was to obtain information that will enable EPA to develop emission factors (for as many HAPs as possible) which will apply to electric utilities employing oil-fired combustion sources. EPA will include these results in a report for Congress. The specific objectives were:
Measure HAP emissions (using methods based on FTIR spectrometry) in
two concentration ranges, near 1 ppm and higher using gas phase
analysis, and at sub-ppm levels using sample concentration/thermal
desorption.
Determine maximum possible concentrations for undetected HAPs based
on detection limits of instrumental configuration and limitations
imposed by composition of flue gas matrix.
Measure O2, CO2, CO, and hydrocarbons using gas analyzers.
Perform simultaneous testing at the inlet and outlet of the ESP and
analyze data to assess the effect (if any) of the control device on
HAP (and other pollutant) emissions.
Obtain process information from LILCO. This information includes
the rate of power production during the test periods and operating
parameters of the control device.
Table 3-1 presents the test schedule that was followed. On set-up day LILCO reported a possible steam leak in Unit 1 that could have led to a shut-down of the unit. After consultation with LILCO, and EPA, Entropy accelerated the schedule to complete the test in two days instead of three. Runs 1 and 2 were performed on July 20 and Run 3 was performed on July 21. 3.3.1 FTIR Results Gas phase and sample concentration data were analyzed for HAPs and other species. All spectra were inspected and absorbance bands identified where possible. Spectra were analyzed, using procedures developed by Entropy, to quantify detected species. The results are presented in Tables 3-2 and 3-3. Maximum possible (minimum detectible) concentrations were determined for undetected HAPs. These results are presented in Tables 3-4, 3-5, 3-6, and 3-7. 3.3.1.1 Gas Phase Results -- Each gas phase sample was analyzed for HAPs and other species. The spectra revealed that the gas phase samples were composed of:
water vapor was detected but quantified with the wet bulb/dry bulb
method.
CO2 was detected but quantified using a CEM.
CO was detected but quantified using a CEM.
NO was measured in condenser and diluted hot/wet samples at an
average concentration of about 210 ppm. Water interference was too
high in the undiluted hot/wet samples to quantify NO.
NO2 was detected in some of the spectra but not quantified because
Entropy does not have reference spectra for NO2. Entropy will
provide NO2 concentrations in the Final report.
SO2 concentrations ranged from about 460 to 540 ppm with no
significant difference between the inlet and outlet of the ESP.
A set of subtracted spectra was generated to analyze for the maximum possible (or minimum detectible) concentrations of undetected HAPs. Reference spectra of water vapor, SO2, NO and CO2 were scaled and subtracted from each sample spectrum. The resulting base lines were analyzed according to procedures described in Section 4.6.3. The upper limit concentration of an undetected compound is referred to in Tables 3-4 to 3-6 as the maximum possible concentration. This quantity was calculated for HAPs in the reference library. Results for hot/wet, condenser and diluted samples (diluted with dry N2 at about 2:1) are presented in Tables 3-4, 3-5, and 3-6, respectively. The results are averages of the calculated values for all of the spectra in the sample runs. Hot/wet gas phase spectra are the most difficult to analyze due to spectral interference from water vapor. Even so, in results from the hot/wet gas phase data, 81 compounds gave minimum detectible concentrations below 10 ppm; of these, 65 are below 5 ppm, and 21 are 1 ppm or lower. For the validation study1 Entropy developed analysis programs for HAPs in flue gas from a coal-fired boiler. Statistical analysis showed the programs to be successful in measuring some HAPs in hot/wet and condenser samples[1]. The major interferant species in coal-fired boiler emissions are similar to those identified in the oil-fired boiler effluent. Therefore, the same programs were used to analyze the data obtained in this test. The results of the analysis are presented in Appendix C. 3.3.1.2 Sample Concentration Results -- Sample concentration spectra are integrated samples collected over each 4-hour run. The samples were composed of:
Water vapor was present but at lower levels than in gas phase
samples so spectral interference was reduced.
Some CO2 remained in the desorbed samples, but most of it was
removed so spectral interference from CO2 was greatly reduced. The
gas analyzer provides a more accurate measure of the CO2
concentration.
Some CO remained in the desorbed samples but was more accurately
measured using the gas analyzer.
Trichlorofluoromethane (CCl3F) was identified in all samples
including the ambient runs and may be a contaminant.
SO2 was detected in samples from all three runs at both locations,
but the sample concentration process removes most of the SO2. A
more reliable measure of the SO2 concentration is provided by the
gas phase results.
HCl was detected in the samples from Run 2 at the ESP inlet and
outlet. HCl is volatile and does not adhere to Tenax® well:
therefore, sample concentration provides a lower limit to the HCl
concentration. The upper limit to the HCl concentration is between
0.8 and 1.3 ppm (Table 3-4) determined from the hot/wet gas phase
data.
Hexane was identified in all samples including the ambient runs.
Features similar to hexane are usually observed in spectra of
desorbed samples and probably include contributions from hexane and
other (higher molecular weight) aliphatic hydrocarbons that were
not completely removed from the Tenax® in the pre-cleaning
procedure.
A cyclic siloxane compound was detected in the samples from Runs 1
and 3 at the ESP inlet and in samples from Runs 1 and 2 at the ESP
outlet. Entropy identified this compound in spectra of samples
taken at the coal-fired boiler validation test[1]. This compound was
shown to be a product of a reaction between HCl or water vapor in
the gas stream and materials in the filter housing of the Method 5
box. Entropy took steps to eliminate this problem and the
siloxane, if it is a contaminant, is present at very low levels (in
the samples from LILCO) relative to validation data.
Formaldehyde was detected in the sample from Run 1 at the ESP
outlet and in one of the ambient samples. Formaldehyde is volatile
and does not adhere to Tenax® well: therefore, sample concentration
provides a lower limit to the formaldehyde concentration. The
upper limit to the formaldehyde concentration is between 1 and 1.4
ppm (Table 3-4) determined from the hot/wet gas phase data.
Table 3-3 presents calculated results for SO2, HCl, formaldehyde, hexane, and CCl3F in samples where these species were detected. The concentration of CCl3F was estimated using a spectrum supplied by Infrared Analysis Inc. The flue gas concentrations were determined using procedures described in Section 4.6.5. The adsorption/desorption efficiencies of light compounds such as HCl and formaldehyde have not been considered. Therefore, the values in Table 3- 3 are lower limit concentrations. Upper limits on HAP concentrations are provided by the analysis of the gas phase data (Tables 3-4, 3-5, and 3-6). Table 3-7 gives minimum detectible concentrations for HAPs undetected in the Tenax® samples. The minimum detectible flue gas concentrations were derived from amount of gas sampled (Sections 4.6.3 and 4.6.5) and are presented in Table 3-7. Additional absorbance features were observed but not identified. None of these features were attributed to HAPs listed Table 3-7. Relative band intensities vary among the sample spectra. Spectral analysis programs were previously developed for sample concentration spectra for analysis of validation data[1]. The programs were used to evaluate sample concentration data for HAPs. The results, presented in Appendix C, give calculated concentrations for HAPs that Entropy used in spiking experiments with Tenax®. 3.3.2 Instrumental and Manual Test Results Table 3-8 summarizes the results obtained using EPA test methods as described in Sections 4-3 and 4-4. All concentration results in the table were determined from the average gas concentration measured during the run and adjusted for drift based on the pre- and post-run calibration results (Equation 6C-1 presented in EPA Method 6C, Section 8). Although not required by Methods 10 and 25A, the data reduction procedures of Method 6C were used for the CO and HC determinations to ensure data quality. All measurement system calibration bias and calibration drift checks for each test run met the applicable specifications of the Methods. Each emission rate value (expressed in units of lb/hr) was computed using the averaged concentration measurement for the test period, flue gas volumetric flow rate, and the appropriate conversion factors. The dry flue gas volumetric flow rates are expressed in units of "dry standard cubic feet per minute (dscfm)." The SO2, NOx, and CO emission rates were computed using the dry basis concentration and flow rate data. Because Method 25A requires that the measurement be made on a wet basis, the wet flow rate results in units of "wet standard cubic feet per minute (wscfm)" were used to compute HC emission rates (lb/hr as methane). 3.3.3 Process Results 3.3.3.1 Operating Conditions -- Process data are presented in Tables in Appendix B and are summarized in Figures 3-1, 3-2, and 3-3. 3.3.3.2 Problems and/or Variations During Sampling -- During Runs 1 and 2, some ESP cells were inoperative. This did not present a problem because no more than one of the eight cells monitored (Figure 2-2) was down at any one time. Otherwise during Run1 (11:00 a.m. to 3:00 p. m., 7/20/93), Run 2 (3:20 p. m. to 7:20 p. m., 7/20/93), and Run3 (100:20 a. m. to 2:20 p. m., 7/21/93), the plant operated at a steady state without notable problems. 3.3.3.3 Calculation of ESP Parameters -- Because the secondary voltage was not displayed on any plant instrumentation, it was derived as shown below. First, to obtain the apparent rectifier efficiency, the ratio of the input ratings to the nominal output ratings of the transformer-rectifier sets was used. Input ratings:
87.5 amperes x 460 Volts = 40,250 Watts
Nominal output ratings:
550 DC milliamperes x 45 KV DC = 24,750 Watts
Apparent rectifier efficiency:
24,750 / 40,250 = .615 = 61.5%
The apparent rectifier efficiency and the recorded parameters: primary
current, primary voltage, and secondary current were combined in equation 1
to calculate the secondary voltage.
where:
V2 = Secondary voltage (kV DC)
RE = Rectifier efficiency
V1 = Primary voltage (V)
I1 = Primary current (amps AC)
I2 = Secondary Current (mAmps DC)
In the following example calculation a rectifier efficiency of 61.5 percent
is assumed:
The measured secondary currents and the derived secondary voltages for each 15 minute monitoring interval were averaged. These averaged numbers were multiplied together to obtain the average corona power input used by an ESP cell during the emissions test. The average corona power input was used in two calculations. In the first, all average corona power inputs were combined to obtain the total average corona power input, which was then divided by the total plate area (ft2) to obtain the total average corona power density. In the second calculation, the average corona power input (for each cell) was divided by each cell's plate area. This calculation provided the average cell corona power density. The result, along with the total average corona power density, is shown in Figures 3-4, 3-5, and 3-6 for Runs 1, 2 and 3, respectively.
Because the number of plates and their sizes were known, the surface area of each cell was determined to aid in visual representation of ESP performance as a function of power distribution. Example:
Active Collection Plate Size
A, B, C Fields - 30' x 6' x 41 plates x 2 sides x 6 cells = 88,560 ft2
D Fields - 30' x 3' x 41 plates x 2 sides x 2 cells = 14,760 ft2
Total Collection Area = 88,560 ft2 + 14,760 ft2 = 103,320 ft2 (South side only)
The collection area for each cell would then be:
A, B, C Fields - 88,560 ft2 / 6 = 14,760 ft2 each
D Fields - 14,760 ft2 / 2 = 7,380 ft2 each
4.0 SAMPLING AND ANALYTICAL PROCEDURESThe FTIR analysis is done using two different experimental techniques. The first, referred to as gas phase analysis, involves transporting the gas stream to the sample manifold so it can be sent directly to the infrared cell. This technique provides a sample similar in composition to the flue gas stream at the sample point location. Some compounds may be affected because of contact with the sampling system components or reactions with other species in the gas. A second technique, referred to as sample concentration, involves concentrating the sample by passing a measured volume through an absorbing material (Tenax®) packed into a U-shaped stainless steel collection tube. After sampling, the tube is heated to desorb any collected compounds into the FTIR cell. The desorbed sample is then diluted with nitrogen to one atmosphere total pressure. Concentrations of species detected in the absorption cell are related to flue gas concentrations by comparing the volume of gas collected to the volume of the FTIR cell. Desorption into the smaller FTIR cell volume provides a volumetric concentration which gives a corresponding increase in analytical sensitivity for the detection of species that can measured using Tenax®. Infrared absorbance spectra of gas phase and concentrated samples were recorded and analyzed. In conjunction with the FTIR sample analysis, measurements of hydrocarbons (HC), carbon monoxide (CO), oxygen (O2), and carbon dioxide (CO2) were obtained using gas analyzers. Components of the emission test systems used by Entropy for this test program are described below. 4.1 EXTRACTIVE SYSTEM FOR DIRECT GAS PHASE ANALYSIS An extractive system, shown in Figure 4-1, was used to transport the gas stream to the infrared cell. 4.1.1 Sampling System Flue gas was extracted through a heated stainless steel sample probe. A Balston® particulate filter rated at 1 micron was installed at the outlet of the probe. The probe was connected to the heated sample pump in the FTIR truck (KNF Neuberger, Inc. model number N010 ST.111) using 3/8-in O.D. Teflon® sample line. The temperature of the sampling system components and transport lines was maintained at about 300 degF using digital temperature controllers. All connections were wrapped with electric heat tape and insulated to eliminate "cold spots" in the sampling system where sample might condense. All components of the sample system were constructed of Type 316 stainless steel or Teflon®. A heated manifold, in the FTIR truck, included a secondary particulate filter and valves that allowed the operator to send sample gas directly to the absorption cell or through a gas conditioning system. The extractive system can deliver three types of samples to the absorption cell. Sample sent directly to the FTIR cell is considered unconditioned, or "hot/wet." This sample is thought to be most representative of the actual effluent composition. The removal of water vapor from the gas stream before analysis was sometimes desirable; therefore, a second type of sample was provided by directing gas through a condenser system. The condenser employed a standard Peltier dryer to cool the gas stream to approximately 38 degF. The resulting condensate was collected in two traps and removed from the conditioning system with peristaltic pumps. This technique is known to leave the concentrations of inorganic and highly volatile compounds very near to the (dry-basis) stack concentrations. A third type of sample was obtained by dilution. The cell was partially filled with sample gas and the partial pressure of the sample was measured and recorded. The cell was then filled to ambient pressure using dry nitrogen. The procedure could be reversed with the nitrogen being introduced to the cell first. A dilution factor of 2:1 significantly reduced spectral interference from water vapor without removing any species from the sample while minimizing the possibility of reducing HAP concentrations below detectible levels. Lowering the water vapor concentration, in addition to protecting the absorption cell components, relieved spectral interferences, which could limit the effectiveness of the FTIR analysis for particular compounds. 4.1.2 Analytical System The FTIR equipment used in this test consists of a medium-resolution interferometer, heated infrared absorption cell, liquid nitrogen cooled mercury cadmium telluride (MCT) broad band infrared detector, and computer (Figure 4-2). The interferometer, detector, and computer were purchased from KVB/Analect, Inc., and comprise their base Model RFX-40 system. The nominal spectral resolution of the system is one wavenumber (1 cm-1). Samples were contained in a model 5-22H infrared absorption cell manufactured by Infrared Analysis, Inc. The inside walls and mirror housing of the cell were Teflon® coated. Cell temperature was maintained at 240 degF using heated jackets and temperature controllers. The absorption path length of the cell was set at 22 meters. 4.1.3 Sample Collection Procedure During all three test runs, gas phase analysis was performed at the ESP inlet and outlet concurrent with the sample concentration testing. The test schedule is presented in Table 3-1. During a 4-hour run, flue gas continuously flowed through the heated system to the sample manifold in the FTIR truck. A portion of the gas stream was diverted to a secondary manifold located near the inlet of the FTIR absorption cell (Figure 4-2). The cell was filled with sample to ambient pressure and the spectrum recorded. The cell was then evacuated to prepare for a subsequent sample. The process of filling the cell, collecting the spectrum and evacuating the cell took less than 10 minutes. During each run, 12 gas phase samples were analyzed. Sample concentration was performed using the adsorbent material Tenax®, followed by thermal desorption into the FTIR cell. The sample collection system employed equipment similar to that of the Modified Method 5 sample train. 4.2.1 Sampling System Figure 4-3 shows the apparatus used in this test program. Components of the sampling train included a heated stainless steel probe, heated filter and glass casing, stainless steel air-cooled condenser, stainless steel adsorbent trap in an ice bath, followed by two water-filled impingers, a knockout impinger, impinger filled with silica gel, sample pump, and a dry gas meter. All heated components were kept at a temperature above 120 degC to ensure no condensation of water vapor within the system. The stainless steel condenser coil was used to pre-cool the gas before it entered the adsorbent trap. The trap was a stainless steel U-shaped collection tube filled with 10 g of Tenax® and plugged at both ends with glass wool. Stainless steel was used to make the adsorbent tubes because it gives a more uniform and more efficient heat transfer than glass. A run lasted 4-hours with a sample flow rate of 0.12 to 0.17 dcfm for a total volume of about 30 to 40 dcf. The sampling rate depended on the sampling train used and was the maximum that could be achieved. Collection times provided a volumetric concentration that was proportional to the volume sampled. The resulting increase in sensitivity allowed detection of some HAPs to concentrations below 1 ppm. 4.2.2 Analytical System Before analysis condensed water vapor was removed from the collection tubes using a dry nitrogen purge for about 15 minutes. Sample analysis was performed using thermal desorption. The sample tubes were wrapped with heat tape and placed in an insulated chamber. One end of the tube was connected to the inlet of the evacuated FTIR absorption cell. The same end of the tube that served as the inlet during the sample concentration run served as the outlet for the thermal desorption. Gas samples were desorbed by heating the Tenax® to 250 degC. A preheated stream of UPC grade nitrogen was passed through the adsorbent and into the FTIR absorption cell. About 7 liters of nitrogen (at 240 degF) carried the desorbed gases to the cell and brought the FTIR sample to ambient pressure. The infrared spectrum was then recorded. The desorption process was repeated until no evidence of additional desorbed compounds was noted in the spectrum. 4.2.3 Sample Collection Procedure Samples were collected at the inlet and outlet of the ESP. The test schedule is presented in Table 3-1. A sample concentration apparatus was set up at each location and ambient samples were collected to ensure each train contained no significant contamination (Section 5.4.1). Entropy performed leak checks of the system and the start time of the run was synchronized at both locations. Sample flow, and temperatures of the heated box, the dry gas meter, and the tube outlet were monitored continuously and recorded at 10- minute intervals. After 4-hrs the collection tube was removed. the open ends were tightly capped and the tube was stored on ice until it was analyzed. The tubes were analyzed within 12 hours after the run. 4.3 CONTINUOUS EMISSION MONITORING Entropy's extractive measurement system and the sampling and analytical procedures used for the determinations of SO2, NOx, HC, CO, O2, and CO2 conform with the requirements of EPA Test Methods 6C, 7E, 25A, 10, and 3A, respectively, of 40 CFR 60, Appendix B. Two heated sampling systems and a single set of gas analyzers were used to analyze flue gas extracted from the ESP inlet and outlet locations. The analyzers received gas delivered sequentially from the two sample locations. A gas flow distribution manifold downstream of the heated sample pump was used to control the flow to each analyzer. A refrigerated condenser removed water vapor except for samples analyzed for HC. (Method 25A requires a wet basis analysis.) The condenser operated at about 38 degF. Condensate was continuously removed from the traps to minimize contact with the sample. The sampling system included a calibration gas injection point immediately upstream of the analyzers for calibration error checks and also at the outlet of each sample probe for the sampling system bias and calibration drift checks. The mid- and high-range calibration gases were certified by the vendor according to EPA Protocol 1 specifications. Methane in air was used to calibrate the HC analyzer. Table 4-1 presents a list of the analyzers that Entropy used during the test program to quantify the gas concentration levels at the sample point locations. Figure 4-1 is a simplified schematic of Entropy's extractive measurement system. A computer-based data acquisition system was used to provide an instantaneous display of the analyzer responses, compile the measurement data collected each second, calculate data averages over selected time periods, calculate emission rates, and document the measurement system calibrations. Test run values were determined from the average concentration measurements displayed by the gas analyzers during the run and are adjusted based on zero and upscale sampling system bias check results using the equation presented in Section 8 of EPA Method 6C. Flue gas flow rates were determined by different methods at each location. The exhaust duct carrying gases from the air preheater branched into two ducts upstream of the ESP inlet location ( Figure 2-3). Each duct passed through the ESP before the streams were recombined downstream of the ESP outlet before the stack. During set-up day Entropy collected velocity data using both a 3-Dimensional (3-D) pitot probe and a standard S-type pitot probe at the inlet and outlet of the south-side ESP. This information indicated a potential for flow disturbances at the outlet. The ESP inlet location did not show evidence of flow disturbance; therefore, the inlet flow determinations were made in accordance with EPA Methods 1, 2, and 3A. The following plan was adopted to measure the total flow through the ESPs:
Before and during Run 1, 3-D measurements were obtained at the south-
side ESP outlet.
As Run 1 and Run 2 continued, 3-D measurements were obtained at the
north side of the ESP outlet.
After Run 2, flow data were obtained using the 3-D probe at the
south-side ESP outlet.
During Run 3, 3-D measurements were obtained at the north and south
sides of the ESP outlet.
During Runs 1, 2 and 3 Entropy performed flow measurements at the
north and south-side ESP inlet using a standard S-type pitot.
A set of flow measurements was obtained for each run at the ESP outlet locations using the 3-D probe and at the ESP inlet locations using a standard S-type pitot. Table 4-2 presents the schedule of flow measurements. The wet-bulb/dry-bulb technique was used to measure percent moisture in the flue gas. Pitot traverse point locations and measurements made at these points are presented on the data sheets included in Appendix A. The 3-D probe was used to measure off-axial flow disturbances. Measurements were obtained at 11 points through each port (44 data points for each duct) to establish a flow profile in the sampling region. Because of the time required to obtain the 44-point traverses through each duct, it was not practical to perform a complete set of pre- and post-run velocity measurements on the north and south sides. During the test runs, an S-type pitot tube was positioned adjacent to the point where the sample concentration probe was inserted. Single point P values were recorded at 10 minute intervals to verify that flow characteristics, at the sampling point, were not changing significantly during the run. During test runs, a representative from RTI monitored plant operations. Process observations are described in Section 3.3.3. 4.6.1 Description of K-Matrix Analyses K-type calibration matrices were used to relate absorbance to concentration. Several descriptions of this analytical technique can be found in the literature[2]. The discussion presented here follows that of Haaland, Easterling, and Vopicka[3]. For a set of m absorbance reference spectra of q different compounds over n data points (corresponding to the discrete infrared wavenumber positions chosen as the analytical region) at a fixed absorption pathlength b, Beer's law can be written in matrix form as where:
A = The n x m matrix representing the absorbance values of the m
reference spectra over the n wavenumber positions, containing
contributions from all or some of the q components;
K = The n by q matrix representing the relationship between absorbance
and concentration for the compounds in the wavenumber region(s) of
interest, as represented in the reference spectra. The matrix
element Knq = banq, where anq is the absorptivity of the qth
compound at the nth wavenumber position;
C = The q x m matrix containing the concentrations of the q compounds
in the m reference spectra;
E = The n x m matrix representing the random "errors" in Beer's law for
the analysis; these errors are not actually due to a failure of
Beer's law, but actually arise from factors such as
misrepresentation (instrumental distortion) of the absorbance
values of the reference spectra, or inaccuracies in the reference
spectrum concentrations.
The quantity which is sought in the design of this analysis is the matrix K, since if an approximation to this matrix, denoted by K, can be found, the concentrations in a sample spectrum can also be estimated. Using the vector A* to represent the n measured absorbance values of a sample spectrum over the wavenumber region(s) of interest, and the vector C to represent the j estimated concentrations of the compounds comprising the sample, C can be calculated from A* and K from the relation Here the superscript t represents the transpose of the indicated matrix, and the superscript -1 represents the matrix inverse. The standard method for obtaining the best estimate K is to minimize the square of the error terms represented by the matrix E. The equation represents the estimate K which minimizes the analysis error. Reference spectra for the K-matrix concentration determinations were deresolved to 1.0 cm-1 resolution from existing 0.25 cm-1 resolution reference spectra. This was accomplished by truncating and reapodizing[4] the interferograms of single beam reference spectra and their associated background interferograms. The processed single beam spectra were recombined and converted to absorbance (see Section 4.3). 4.6.2 Preparation of Analysis Programs To provide accurate quantitative results, K-matrix input must include absorbance values from a set of reference spectra which, added together, qualitatively model the appearance of the sample spectra. For this reason, all of the Multicomponent analysis files included spectra representing interferant species and criteria pollutants identified in the flue gas. Several factors affect the detection and analysis of an analyte in the flue gas matrix. One factor is the gas composition. The major spectral interferants in oil-fired boiler effluent are water and CO2. At CO2 concentrations of 10 percent and higher, weak absorbance bands become visible. Portions of the spectrum could not be analyzed because of absorbance features from water and CO2, but most compounds exhibit at least one absorbance band that is suitable for analysis. Significant amounts of SO2, NO, and NO2 were also present in the samples and these species must be considered in the analysis. A second factor is the number of analytes detected in the sample. The analytical program becomes more limited in distinguishing overlapping bands as the spectra become more complicated. A third factor depends on how well the sample spectra are modeled. Spectra are best analyzed when all the observed bands are accounted for using with reference spectra. If a major component is identified and its reference spectrum is unavailable then the analysis of other species in the sample may be complicated. Before K-matrix analysis was applied to data, all of the spectra were inspected to identify the components of the sample. Entropy prepared program files to measure the detected species. Four baseline subtraction points were specified in each analytical region, identifying an upper and a lower baseline averaging range. The absorbance data in each range were averaged, a straight baseline was calculated through the range midpoint using the average absorbance values, and the baseline was subtracted from the absorbance values prior to K-matrix analysis. Gas phase and sample concentration spectra were analyzed using K-matrix analysis. 4.6.3 Error Analysis of data The principal constituents of the gas phase samples were water, CO2, SO2, NO, and NO2. A program file was prepared to quantify each of these compounds. Other than these species and N2O no major absorbance features were observed in the gas phase spectra. After concentrations of the main constituents were determined, the appropriate standard was scaled and subtracted from the spectrum of the sample mixture. This helped verify the calculated concentrations and generated a base line by successively subtracting scaled standard spectra of water, CO2, SO2, NO, and NO2. The resulting "subtracted" spectrum was analyzed for HAPs and used to calculate maximum possible concentrations for undetected HAPs. Maximum possible (minimum detectible) concentrations were determined in several steps. The noise level in the appropriate analytical region was quantified by calculating the root mean square deviation (RMSD) of the baseline in the subtracted spectrum. The RMSD was multiplied by the width (in cm-1) of the analytical region to give an equivalent "noise area" in the subtracted spectrum. This value was compared to the integrated area of the same analytical region in a standard spectrum of the pure compound. The noise was calculated from the equation: where:
RMSD = Root mean square deviation in the absorbance values within a
region.
n = Number of absorbance values in the region.
Ai = Absorbance value of the ith data point in the analytical
region.
AM = Mean of all the absorbance values in the region.
The error in the calculated concentration of a detected compound is given by: where:
Eppm = Noise related error in the calculated concentration, in ppm.
x2 = Upper limit, in cm-1, of the analytical region.
x1 = Lower limit, in cm-1, of the analytical region.
AreaR = Total band area (corrected for path length, temperature, and
pressure) in analytical region of reference spectrum of
compound of interest.
CONR = Known concentration of compound in the same reference
spectrum.
This ratio provided a concentration equivalent of the measured area in the subtracted spectrum. For undetected compounds, Eppm is equivalent to the maximum possible concentration in the sample. Some concentration limits given in Tables 3-4 to 3-6 are relatively high (greater than 10 ppm) and there are several possible reasons for this.
The reference spectrum of the compound may show low absorbance at
relatively high concentrations so that its fundamental limit of
detection is relatively high.
The region of the spectrum used for the analysis may have residual
bands or negative features resulting from spectral subtraction. In
these cases the absorbance of the reference band may be large at low
concentrations, but the RMSD is also large (Equation 7). Condenser
samples often give lower Eppm than hot/wet samples because it is easier
to spectrally subtract water vapor from the dry sample. However, the
Eppm calculated for hot/wet spectra are often more reliable because
some compounds do not pass through the condenser.
The chosen analytical region may be too large, unnecessarily
including regions of noise where there is no absorbance from the
compound of interest.
In the second and third cases Eppm may be lowered by choosing a different analytical region, generating better subtracted spectra, or by narrowing the limits of the analytical region. Entropy took these steps to minimize the maximum possible HAP concentrations presented in Section 3.3.1. 4.6.4 Concentration Correction Factors Calculated sample concentrations were corrected for differences in absorption pathlength between the reference and sample spectra according to the following relation: where: Ccorr = The pathlength corrected concentration. Ccalc = The initial calculated concentration (output of the Multicomp program designed for the compound) Lr = The pathlength associated with the reference spectra. Ls = The pathlength (22m) associated with the sample spectra. Ts = The absolute temperature of the sample gas (388 K). Tr = The absolute gas temperature at which reference spectra were recorded (300 to 373 K). Corrections for variation in sample pressure were considered, and found to affect the indicated concentrations by no more that one to two percent. Since this is a small effect in comparison to other sources of analytical error, no sample pressure corrections were made. 4.6.5 Analysis of Sample Concentration Spectra Sample concentration spectra were analyzed in the same way as gas phase data. Flue gas concentrations were derived by dividing the calculated concentrations by the concentration factor (CF). To illustrate, suppose that 10 ft3 (about 283 liters) of gas were sampled and then desorbed into the FTIR cell volume of approximately 8.5 liters to give concentration factor of about 33. If a HAP is detected at 50 ppm in the FTIR cell, its corresponding flue gas concentration is about 1.5 ppm. The volume of flue gas sampled was determined from the relation: where:
Vflue = Total volume of flue gas sampled.
Vcol = Volume of gas sampled as measured at the dry gas meter after
it passed through the collection tube.
Tflue = Absolute temperature of the flue gas at the sampling location.
Tcol = Absolute temperature of the sample gas at the dry gas meter.
W = Fraction (by volume) of flue gas stream that was water vapor.
The concentration factor, CF, was determined using Vflue and the volume of the FTIR cell, Vcell: The flue gas concentration was determined using CF and the concentration in the FTIR sample, Ccell. 5.0 INTERNAL QUALITY ASSURANCE/QUALITY CONTROL ACTIVITIESQuality control (QC) is defined as a system of activities designed to ensure a quality product or service. This may include routine procedures for obtaining prescribed standards of performance in the monitoring and measurement process. Quality assurance (QA) is defined as a system of activities that provides a mechanism of assessing the effectiveness of the quality control procedures. It is an integrated program for assuring the reliability of monitoring and measurement data. The specific internal QA/QC procedures that were used during this test program to produce useful and valid data are described in this section. Each procedure was an integral part of the test program activities. 5.1 QC PROCEDURES FOR MANUAL FLUE GAS TEST METHODS This section details the QC procedures followed for manual test activities. 5.1.1 Velocity/Volumetric Flow Rate QC Procedures The QC procedures for velocity/volumetric flow rate determinations followed guidelines set forth by EPA Method 2. Incorporated into this method are sample point determinations by procedures of EPA Method 1. Gas moisture content was approximated using the wet bulb-dry bulb technique. The following QC steps were followed during these tests:
The S-type pitot tube was visually inspected before sampling.
Both legs of the pitot tube were leak checked before and after
sampling.
Proper orientation of the S-type pitot tube was maintained while
making measurements. The roll and pitch axis of the S-type pitot
tube was maintained at 90 deg to the flow.
The magnehelic set was leveled and zeroed before each run.
The pitot tube/manometer umbilical lines were inspected before and
after sampling for leaks and moisture condensate (lines were cleared
if found).
Cyclonic or turbulent flow checks were performed prior to testing the
source.
Reported duct dimensions and cross-sectional duct area were verified
by on-site measurements.
If a negative static pressure was present at sampling ports, checks
were made for air in-leakage at the sample port which could have
resulted in possible flow and temperature errors. Leaks were sealed
when found.
The stack gas temperature measuring system was checked by observing
ambient temperatures prior to placement in the stack.
The QC procedures followed to ensure accurate sample gas volume determination are:
The dry gas meter is fully calibrated every 6 months using an EPA
approved intermediate standard.
Pre-test and post-test leak checks were completed and were less than
0.02 cfm or 4 percent of the average sample rate.
The gas meter was read to a thousandth (.001) of a cubic foot for the
initial and final readings.
Readings of the dry gas meter, meter orifice pressure ( H), and meter
temperatures were taken every 10 minutes during sample collection.
Accurate barometric pressures were recorded at least once per day.
Post-test dry gas meter checks were completed to verify the accuracy
of the meter full calibration constant (Y).
5.1.2 Sample Concentration Sampling QC Procedures QC procedures that allowed representative collection of organics by the sample concentration sampling system were:
Only properly cleaned glassware and prepared adsorbent tubes that had
been kept closed with stainless steel caps were used for any sampling
train.
The filter, Teflon® transfer line, and adsorbent tube were maintained
at +-10 degF of the specified temperatures.
An ambient sample was analyzed for contamination in the sample train.
Clean sample tubes were analyzed for contamination prior to their use
for sampling.
5.1.3 Manual Sampling Equipment Calibration Procedures 5.1.3.1 Type-S Pitot Tube Calibration -- EPA has specified guidelines concerning the construction and geometry of an acceptable Type-S pitot tube. If the specified design and construction guidelines are met, a pitot tube coefficient of 0.84 is used. Information pertaining to the design and construction of the Type-S pitot tube is presented in detail in Section 3.1.1 of EPA document 600/4-77-027b. Only Type-S pitot tubes meeting the required EPA specifications were used. The pitot tubes were inspected and documented as meeting EPA specifications prior to field sampling. 5.1.3.2 Temperature Measuring Device Calibration -- Accurate temperature measurements are required during source sampling. The bimetallic stem thermometers and thermocouple temperature sensors used during the test program were calibrated using the procedure described in Section 3.4.2 of EPA document 600/4-77-027b. Each temperature sensor is calibrated at a minimum of three points over the anticipated range of use against a NIST-traceable mercury-in-glass thermometer. All sensors were calibrated prior to field sampling. 5.1.3.3 Dry Gas Meter Calibration -- Dry gas meters (DGMs) were used in the sample trains to monitor the sampling rate and to measure sample volume. All DGMs were fully calibrated to determine the volume correction factor prior to their use in the field. Post-test calibration checks were performed as soon as possible after the equipment was returned as a QA check on the calibration coefficients. Pre- and post-test calibrations should agree within 5 percent. The calibration procedure is documented in Section 3.3.2 of EPA document 600/4-77-237b. 5.1.3.4 3-Dimensional Probe Calibration -- The following QC procedures were performed when using the 3-dimensional probe.
The barometric pressure was recorded daily.
The entire sampling system was leak checked prior to each run.
The direction of gas flow will be determined before sampling.
The angle finder was determined to be working properly.
The manometers were leveled and zeroed every day.
The probe was positioned at the measurement point and rotated in the
gas stream until zero deflection is indicated for the yaw angle; this
null position occurs when P2 = P3. Each yaw angle reading from the
protractor or other angle measuring device was recorded.
Holding the null position, readings were taken and recorded for the
(P1 - P2) and (P4 P5). The tester recorded the duct pressure or the
(P2 - Pbar).
The procedure was repeated at each measurement point.
The pitch angle was determined from the F1 calibration curve and F2
was determined from the F2 calibration curve.
Calibration curves were generated from the procedures outlined in
Draft Method 2E.
5.2 QC PROCEDURES FOR INSTRUMENTAL METHODS Flue gas was analyzed for carbon monoxide (CO), oxygen (O2), carbon dioxide (CO2) and hydrocarbons (HC). Prior to sampling each day a pre-test leak check of the sampling system from the probe tip to the heated manifold was performed and was less than 4 percent of the average sample rate. Internal QA/QC checks for the CEM systems are presented below. 5.2.1 Daily Calibrations, Drift Checks, and System Bias Checks Method 3A requires that the tester: (1) select appropriate apparatus meeting the applicable equipment specifications of the method, (2) conduct an interference response test prior to the test program, and (3) conduct calibration error (linearity), calibration drift, and sampling system bias determinations during the test program to demonstrate conformance with the measurement system performance specifications. The performance specifica- tions are identified in Table 5-1. A three-point (i.e., zero, mid-, and high-range) analyzer calibration error check is performed before sampling by injecting calibration gases directly into the gas analyzer and recording the responses. Zero and upscale calibration checks are conducted both before and after each run to quantify measurement system calibration drift and sampling system bias. Upscale is either the mid- or high-range gas, whichever most closely approximates the flue gas level. During these checks, the calibration gases are introduced into the sampling system at the probe outlet and analyzed in the same manner as the flue gas samples. Drift is the difference between the pre- and post- test run calibration check responses. Sampling system bias is the difference between the test run calibration check responses (system calibration) and the initial calibration error responses (direct analyzer calibration) to the zero and upscale calibration gases. If an acceptable post-test bias check result is obtained but the zero or upscale drift result exceeds the drift limit, the test run result is valid; however, the analyzer calibration error and bias check procedures must be repeated before the next test run. A run is considered invalid and must be repeated if the post-test zero or upscale calibration check result exceeds the bias specification. The calibration error and bias checks must be repeated and acceptable results obtained before testing can resume. Although not required by Methods 10 and 25A, the same calibration and data reduction procedures required by Method 3A were used for the CO and HC determinations to ensure the quality of the reference data. 5.3 QA/QC CHECKS FOR DATA REDUCTION, VALIDATION, AND REPORTING Data quality audits were performed using data quality indicators which require the detailed review of: (1) the recording and transfer of raw data; (2) data calculations; (3) the documentation of procedures; and (4) the selection of appropriate data quality indicators. All data and/or calculations for flow rates, moisture content, and sampling rates were spot checked for accuracy and completeness. In general, all measurement data have been validated based on the following criteria:
acceptable sample collection procedures
adherence to prescribed QC procedures.
Any suspect data have been identified with respect to the nature of the problem and potential effect on data quality. Upon completion of test, the field coordinator was responsible for preparation of a data summary including calculation results and raw data sheets. 5.3.1 Sample Concentration The sample concentration custody procedures for this test program were based on EPA recommended procedures. Because collected samples were analyzed on-site, the custody procedures emphasized careful documentation of sample collection and field analytical data. Use of chain-of-custody documentation was not necessary. Instead, careful attention was paid to the sample identification coding. These procedures are discussed in more detail below. Each sample concentration spectrum was assigned a unique alphanumeric identification code. For example, Tinl102A designates a desorption spectrum of a Tenax® sample taken at the ESP inlet during Run 1 using tube number 02. The A indicates this was the spectrum of the first desorption from this sample. Every collection tube was inscribed with an identification number. The project manager was responsible for ensuring that proper custody and documentation procedures were followed for the field sampling, sample recovery, and for reviewing the sample inventory after each run to ensure complete and up-to-date entries. A sample inventory was maintained to provide an overview of all sample collection activities. Every sample tube was cleaned and checked for contamination before use. The contamination check consisted of desorbing the clean tube and recording its spectrum. Each sampling train was checked for contamination before the test and after all test runs were completed. The trains were set up according to the procedures of Section 4.2, except that the probe was not inserted into the port. Ambient air was drawn through the entire sample concentration apparatus for one hour. This time was sufficient to reveal significant contamination on the system components. About 10 ft3 of air was sampled for the ambient checks. The ambient tube was stored and analyzed in the same way as the sample tubes. Minor contamination was accounted for in the subsequent analysis by using spectral subtraction. Evidence of major contamination was not identified in any sample. Sample flow at the dry gas meter was recorded at 10 minute intervals. Results from the analyzers and the spectra of the gas phase samples provided a check on the consistency of the effluent composition during the sampling period. 5.3.2 Gas Phase Analysis During each run at least 12 gas phase samples were collected and analyzed. Each spectrum was assigned a unique file name and a separate data sheet identifying sample location and sampling conditions. A comparison of all spectra in this data set provided information on the consistency of effluent composition and a real-time check on the performance of the sampling system. Effluent was directed through all sampling lines for at least 5 minutes and the CEMs provided consistent readings over the same period before sampling was attempted. This requirement was satisfied when switching to a different conditioning system or between locations. The FTIR continuously scanned when the cell was evacuating to provide a spectral profile of the empty cell. A new sample was not introduced until no residual absorbance features remained from the previous sample. The FTIR also continuously scanned during sample collection to provide a real-time check on possible contamination in the system. 5.3.3 FTIR Spectra For a detailed description of QA/QC procedures relating to data collection and analysis, refer to the "Protocol For Applying FTIR Spectrometry in Emission Testing." A spectrum of the calibration transfer standard (CTS) was recorded and a leak check of the FTIR cell was performed before and after each sampling session. The CTS was 100 ppm ethylene in nitrogen. The CTS spectrum provided a check on the operating conditions of the FTIR instrumentation, e.g. spectral resolution and cell path length. Ambient pressure was recorded whenever a CTS spectrum was collected. Two copies of all interferograms, processed backgrounds, sample spectra, and the CTS were stored on separate computer disks. Additional copies of sample and CTS absorbance spectra were also stored for use in the data analysis. Sample spectra can be regenerated from the raw interferograms, if necessary. FTIR spectra are available for inspection or re-analysis at any future date. Pure, dry ("zero") air was periodically introduced through the sampling system in order to check for contamination or if condensation formed. Once, when water condensed in the manifold, the lines and cell were purged with dry N2, until sampling could continue. The position and slope of the spectral base line was constantly monitored. If the base line within a data set for a particular sample run began to deviate by more than 5 percent from 100 percent transmittance, a new background was collected. During the test program, it was the responsibility of the field coordinator and the team members to ensure that all data measurement procedures were followed as specified and that data met the prescribed acceptance criteria. Specific procedures for corrective actions are described above. 6.0 CONCLUSIONS AND DISCUSSIONEntropy conducted an emission test at LILCO's oil-fired boiler in Northport, New York. Gas phase analysis, and sample concentration were performed over two days. Three 4-hour sample concentrations runs were performed at the ESP inlet and outlet. FTIR gas phase analysis and CEM measurements were performed concurrently with the sample concentration runs. Gas phase analysis revealed the presence of water vapor, CO, CO2, NO2, SO2, and NO. HCl, CCl3F, formaldehyde, hexane, and a cyclic siloxane were detected in concentrated samples from both locations. Also, unidentified absorption bands remain which may be due to species produced in the process. The primary goal of this project was to use FTIR instrumentation in a major test program to measure as many HAPs as possible or to place upper limits on their concentrations. Four other electric utilities were tested along with the LILCO facility. Utilities present a most difficult testing challenge for two reasons:
1) They are combustion sources so the flue gas contains high levels of
moisture and CO2 (both are spectral interferants).
2) The large volumetric flow rates typical of these facilities can lead
to mass emissions above regulated limits even for HAPs at very low
concentrations. This places great demand on the measurement method
to achieve low detection limits.
This program represents the first attempt to use FTIR spectroscopy in such an ambitious test program. The program accomplished very significant achievements and demonstrated important and fundamental advantages of FTIR spectroscopy as an emissions test method over other test methods:
Using a single method quantitative data were provided for over 100
compounds.
Software was written to analyze a large data set and provide
concentration and detection limit results quickly. The same or
similar software can be used for subsequent tests with very little
investment of time for minor modifications or improvements.
The original data are permanently stored so the results can be
rechecked for verification at any time.
A single method was used to obtain both time-resolved (direct gas)
and integrated (sample concentration) measurements of gas streams
from two locations simultaneously.
The two techniques of the FTIR method cover different concentration
ranges.
Preliminary data (qualitative and quantitative) are provided on-site
in real time.
With little effort at optimization (see below), detection limits in
the ppb range were calculated for 21 HAPs and between 1 and 5 ppm for
65 other HAPs using direct gas phase measurements of hot/wet samples,
which present the most difficult analytical challenge. Sample
concentration provided even lower detection limits for some HAPs.
A compound detect is unambiguous.
It is appropriate to include some discussion about the "maximum possible concentrations" presented in Tables 3-4, 3-5, 3-6, and 3-7. These numbers were specifically not labeled as detection limits because use of that term could be too easily misinterpreted. But the numbers in Tables 3-4 to 3-7 will be referred to as "detection limits" in the discussion below. In FTIR analysis detection limits are calculated from the spectra (see Section 4.6.3 and the "FTIR Protocol"). These calculated numbers do not in any way represent fundamental measurement limits, but they depend on a number of factors. For example:
Some instrumental factors
Spectral resolution.
Source intensity.
Detector response and sensitivity.
Path length that the infrared beam travels through the sample.
Scan time.
Efficiency of infrared transmission (through-put).
Signal gain.
Some sampling factors
Physical and chemical properties of a compound.
Flue gas composition.
Flue gas temperature.
Flue gas moisture content.
Length of sample line (distance from location).
Temperature of sampling components.
Sample flow.
Instrumental factors are adjustable. For this program instrument settings were chosen to duplicate conditions that were successfully used in previous screening tests and the validation test. These conditions provide speed of analysis, durability of instrumentation, and the best chance to obtain measurements of the maximum number of compounds with acceptable sensitivity. Sampling factors present the same challenges to any test method. An additional consideration is that the numbers presented in Tables 3-4 to 3-7 are all higher than the true detection limits that can be calculated from the 1 cm-1 data collected at LILCO. This results from the method of analysis: the noise calculations were made only after all spectral subtractions were completed. Each spectral subtraction adds noise to the resulting subtracted spectrum. For most compounds it is necessary to perform only some (or none) of the spectral subtractions before its detection limit can be calculated. With even more sophisticated software it will be possible to automate the process of performing selective spectral subtractions and optimize the detection limit calculation for each compound. (Such an undertaking was beyond the scope of the current project.) Furthermore, the detection limits represent averages compiled from the results of all the spectra collected at a given location. A more realistic detection limit is provided by the single spectrum whose analysis gives the lowest calculated value. It would be more accurate to think of "maximum possible concentrations" as placing upper boundaries on the HAP detection limits provided by these data. Perhaps the most important sampling consideration is the sample composition. In Table 3-4 benzene's detection limit is quoted as 6.56 ppm. This was determined in the analytical region between 3020 and 3125 cm-1. Benzene exhibits a much stronger infrared band at 673 cm-1 but this band was not used in the analysis because absorbance from CO2 strongly interfered in this analytical region. At a lower CO2 emission source an identical FTIR measurement system would provide a benzene detection limit below 1 ppm for direct gas analysis (even ignoring the consideration discussed in the previous paragraph). Data from Tables 3-4 to 3-7 should not be used to calculate mass emission rates because compounds listed in those tables are non-detects. Finally, there may be some question about why certain species were not detected in gas phase samples; particularly HCl. (HCl was measured in both Tenax(r) samples from Run 2, but at very low levels, and these measurements are not quantitative.) One answer could be that HCl concentrations were actually below the lowest stated detection limit of 840 parts per billion (at the ESP inlet). The fuel analysis provided to RTI (Table 2-1) does not include a chloride measure, but for the sake of discussion it will be assumed that HCl was present above 1 ppm in the gas stream at the sampling location, which is detectible by direct FTIR gas analysis, and the question will be explored as to why the HCl in the FTIR sample was not also above 1 ppm so that it could be measured. The sampling system configuration (including the temperatures of components) was chosen because the same configuration was used successfully at other tests. HCl was measured at utilities and other emission sources during the FTIR development project. It was assumed that flue gas conditions would be similar to those at the electric utilities Entropy tested during the development project. In fact, the flue gas at LILCO contained 16 percent moisture. This is much higher that the 7 percent moisture that was encountered when Entropy tested utilities for the screening and validation tests. High moisture makes HCl measurements difficult because it is water soluble. (Entropy has detected HCl in a 22 percent moisture stream using dilution.) Maintaining the sampling system and FTIR cell at a higher temperature would have meant testing under conditions different from those used at the validation. The sample stream could have been spiked with HCl to verify sampling system integrity but this precaution was not considered before the test because it was assumed the moisture content would not be a significant problem. In any event, nothing would have been gained by raising the temperature of the sampling components because the measured flue gas temperature at both locations was between 300 and 320 degF. The sampling system up to the FTIR cell was maintained above 300 degF. The FTIR cell was maintained at 250 degF (to keep spectral conditions near to those of the reference spectra), but this could not have interfered with HCl measurements because there was no condensation in the cell. The important point to emphasize is that these difficulties are all related to the sampling system and have absolutely nothing to do with the FTIR analysis. In fact, FTIR techniques offer the best opportunity to accurately measure HCl (and other unstable or reactive species) because FTIR spectrometry can be readily used to easily and unequivocally monitor the sampling system integrity. That was not done in this test because the primary goal was the general one of measuring as many compounds as possible, not optimizing the measurement system for any particular compound or set of compounds. Furthermore, the testing schedule was compressed by the process difficulties LILCO experienced. This made any further deviation from the plan impossible. All previous studies on HCl sampling and measurement indicate that high sample flow rates are required to deliver HCl to the measurement system. Entropy has participated in EPRI (Electric Power Research Institute) studies performing FTIR CEM measurements at utilities. In these studies HCl was measured using a sample flow of 10-15 lpm and heated lines at 300 degF. At the LILCO test it was not possible to achieve a sample flow rate above 6-7 lpm because, in addition to FTIR testing, Entropy was also delivering sample to five gas analyzers. EPA required CO, CO2, HC, and O2 measurements and a NOx monitor was also used to provide LILCO with data to optimize their process before testing. When FTIR is used as a stand-alone method the sampling demands of similar emissions tests will be greatly reduced. 7.0 REFERENCES1) "FTIR Method Validation at a Coal-Fired Boiler," EPA Contract
No.68D20163, Work Assignment 2, July, 1993. 4) "Fourier Transform Infrared Spectrometry," Peter R. Griffiths and James de Haseth, Chemical Analysis, 83, 16-25,(1986), P. J. Elving, J. D. Winefordner and I. M. Kolthoff (ed.), John Wiley and Sons,. |