EPA On-line Tools for Site Assessment Calculation
| Module Home Objectives Table of Contents Previous < Next > |
| 16 of 67 |
Streamline Location and Plume Diving
Water entering the aquifer at any point, x, along the phreatic surface defined by Bear's aquifer solution would move down gradient and also deeper into the aquifer. The path taken by that water or by a contaminant introduced at that point is shown in Figure~\ref{fig:two}.
Strack (1984)
and
Haitjema (1995)
, showed that at any point, x, in a water table aquifer, the flux is related to the recharge, N, by
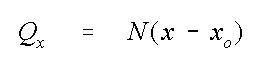
where Qx is the volumetric flow rate per unit width of the aquifer [L3/L/T], and xo is the location of an assumed upgradient stagnation point. This equation holds because all flow in the aquifer is assumed to originate from recharge that entered between an assumed upgradient stagnation point at xo and the down gradient location, x. Further, the flow entering the aquifer between any two points is thus simply the difference between the fluxes at those two points. This fact can also easily be shown from Bear's solution by applying the equation to two points in the aquifer. For example, between the origin of a streamline, xs and a downgradient point, x the added flux, Qx
D is
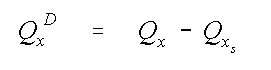
which is taken as water that lies above the streamline.
The flow in the aquifer is partitioned above and below the streamline originating at x = xs by
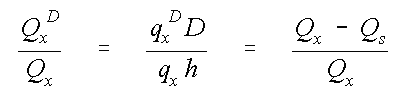
where h is the depth of water at x, and the depth of the streamline below the water table, D, is
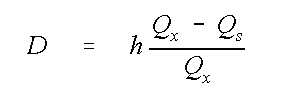
In the second equation, the Dupuit assumption is implicit in the assumption that the ground water velocity was constant over the vertical (i.e., qx
D = qx ). Here all of the recharge entering the aquifer downgradient from the streamline origin lies above the streamline whose depth is equal to D.
Home | Glossary | Notation | Links | References | Calculators |